#640 후기
|
처음 참여한 Div4 코드포스여서 난이도나 이런것들에 대해서 궁금하기도 하고, 많이풀수있을까 기대되기도 했던 코드포스였다. 대회때는 D번까지 풀었고, 이후 생각나서 E번부터 G번까지 마저 풀었는데, 다시 풀어보면서 느낀점은, Div4의 E번부터 G번문제도 생각보다 풀만한 문제구나 느꼈다. |
#640 문제
A번 Sum of Round Numbers - 성공
양수 x가 d000...0 형식인 경우 해당 수는 둥글다(Round)라고 한다. 양수 n을 둥근 수의 합으로 나타냈을 때, 둥근 수의 개수와 둥근 수를 출력하시오.
문제에서 둥근 수의 예를 들어줬는데,
1000, 100, 10, 1과 같이 맨 앞자리수가 1 ~ 9인 자연수이고, 그 뒤에 0이 0개부터 n개 있는 수가 둥근 수이다.
즉, 자릿수가 a개인 정수 n이 주어지면, 자릿수 각각을 확인하면서, 그 자릿수가 0이 아닌경우, 둥근 수로 표현이 가능하다.
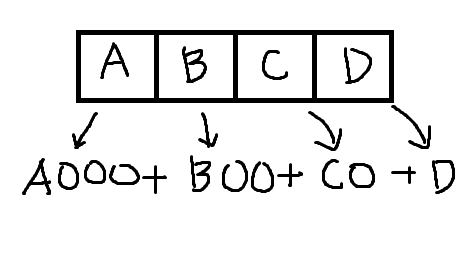
그 자릿수가 0인경우, 분해했을 때, 수가 000...0 꼴이 되므로, 불가능하다.
아래는 제출코드이다.
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
int main(void) {
// For fast IO
cin.tie(NULL);
ios_base::sync_with_stdio(false);
int tc;
string n;
cin >> tc;
while(tc--) {
cin >> n;
int cnt = 0;
for(int i = 0; i < n.size(); i++) {
if(n[i] != '0') cnt++;
}
cout << cnt << "\n";
for(int i = 0; i < n.size(); i++) {
if(n[i] != '0') {
cout << n[i];
for(int j = 0; j < n.size() - i - 1; j++) cout << "0";
cout << " ";
}
}
cout << "\n";
}
return 0;
}B번 Same Parity Summands - 성공
정수 n과 k가 주어진다. 정수 n을 k개의 양의 정수의 합으로 나타내야 하는데, 해당 수들은 모두 같은 패리티(홀수/짝수)여야 한다.
해당 수들의 합으로 나타낼수 있는지와, 나타낼 수 있으면 그 수들을 출력하시오.
조건을 잘 세우고, 그대로 코드를 구현하면 되는 문제지만, 빼먹은 조건이 있어서 대회때는 한번 틀렸었다.
먼저, 문제 조건에서 k가 n보다 크다는 조건이 없으므로, 만약 k가 n보다 크다면 항상 불가능하다는 것을 처리해야 한다.
그리고, n이 짝수일때와, 홀수일때로 나눌 수 있다. 그리고 이때 각각 k가 짝수일때와, 홀수일때로 나눌 수 있다.
짝수끼리의 합은 항상 짝수이다.
그리고 홀수끼리의 합은 짝수일수도, 홀수일수도 있다.
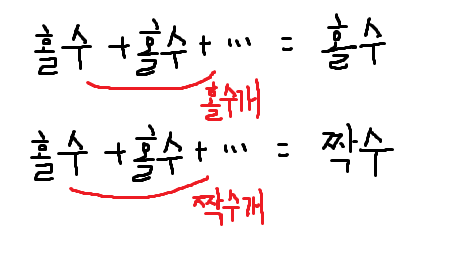
즉 먼저, n이 홀수이고, k가 짝수이면 불가능하다. (짝수개로 홀수를 만들 수 없음)
(n이 홀수, k가 짝수) 라면, 1을 (k - 1)개 출력하고, n에서 (k - 1)만큼 뺀 값을 출력하면 된다.
(n이 짝수, k가 짝수) 라면, 위에서처럼, 짝수개의 홀수의 합은 짝수이므로, 마찬가지로, 1을 (k - 1)개 출력하고, n에서 (k - 1)만큼 뺀 값을 출력하면 된다.
마지막으로 (n이 짝수, k가 홀수) 라면, n을 만들기 위해서는 항상 짝수의 합으로 만들어야 한다.
짝수의 최솟값은 2인데, 위에서처럼 2를 (k - 1)개 출력하고, n에서 2 * (k - 1) 만큼 뺀 값을 출력하면 되지만, 만약 이때 n - 2 * (k - 1) 값이 0 이하가 된다면 불가능한 경우를 의미한다.
아래는 제출코드이다.
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
int main(void) {
// For fast IO
cin.tie(NULL);
ios_base::sync_with_stdio(false);
int tc;
int n, k;
cin >> tc;
while(tc--) {
cin >> n >> k;
if(n < k || (n % 2 != 0 && k % 2 == 0)) {
// k가 n보다 크면 불가능, 홀수를 짝수개로 나누면 불가능
cout << "NO\n";
} else {
// 나머지 케이스
if(n % 2 ==0) {
// n이 짝수면
// k가 짝수면
if(k % 2 == 0) {
int cnt = 0;
for(int i = 0; i < k - 1; i++) {
n = n - 1;
cnt++;
}
cout << "YES\n";
for(int i = 0; i < cnt; i++) {
cout << "1 ";
}
cout << n << "\n";
} else {
// k가 홀수면
int cnt = 0;
for(int i = 0; i < k - 1; i++) {
n = n - 2;
cnt++;
}
if(n <= 0) {
cout << "NO\n";
continue;
}
cout << "YES\n";
for(int i = 0; i < cnt; i++) {
cout << "2 ";
}
if(n != 0) cout << n;
cout << "\n";
}
} else {
cout << "YES\n";
int cnt = 0;
for(int i = 0; i < k - 1; i++) {
n = n - 1;
cnt++;
}
for(int i = 0; i < cnt; i++) {
cout << "1 ";
}
if(n != 0) cout << n;
cout << "\n";
}
}
}
return 0;
}C번 K-th Not Divisible by n - 성공
정수 n과 k를 입력받는다. 양의 정수에 대해서, n으로 나눌 수 없는 k번째 양의 정수를 출력하시오.
n과 k가 각각 10^9까지의 범위에 포함되므로, 최악의 경우에는 정수범위를 초과할 수 있기때문에, long long 형을 이용해서 풀었다.
범위가 넓기 때문에, 이분탐색을 통해 cur가 몇번째 수인지 확인하고, 순서가 적다면 더 큰 값을, 순서가 많앋면 더 작은값을 계속해서 탐색해 나갔다.
코드에서 첫번째 if문은 cur가 n의 배수인 경우를 체크해서, n의 배수인 경우 cur를 1 더해서 확인하였다.
그리고, ncnt는 cur 이전에 n의 배수의 개수를 확인하는 값이고, 결국 cur의 순서는 cur - ncnt가 된다.
순서는 단 하나만 존재하므로, 만약 답을 발견했다면 break로 루프를 빠져나왔고, 그렇지 않으면 위에서처럼 로직에 따라 범위를 계속해서 줄여나갔다.
아래는 제출코드이다.
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
int main(void) {
// For fast IO
cin.tie(NULL);
ios_base::sync_with_stdio(false);
ll tc;
ll n, k;
cin >> tc;
while(tc--) {
cin >> n >> k;
ll l = 0;
ll h = 2000000000 + 1;
ll ret = -1;
while(l <= h) {
ll cur = (l + h) / 2;
if(cur % n == 0) cur++;
ll ncnt = cur / n; // cur에 n의 배수가 몇개 들어가있는지 구함
if(cur - ncnt == k) {
ret = cur;
break;
} else if(cur - ncnt < k) {
// 순서가 더 작을 경우
l = cur + 1;
} else {
h = cur - 1;
}
}
cout << ret << "\n";
}
return 0;
}D번 Alice, Bob and Candies - 성공
길이 n인 정수 배열이 주어진다. 배열 각각에는 캔디의 크기가 주어진다. Alice는 왼쪽부터, Bob은 오른쪽부터 캔디를 먹기 시작한다. 처음에 Alice가 가장 왼쪽칸의 캔디를 먹는다. 이후 Bob은 오른쪽부터 Alice가 먹은 캔디의 크기보다 많은 크기를 먹는다. 이후 Alice도 Bob이 먹은 캔디의 크기보다 많은 크기를 먹어야 한다. 이 과정이 불가능할때까지 캔디를 먹었을 때, Alice가 먹은 총 사탕의 크기와 Bob이 먹은 총 사탕의 크기를 출력하시오.
문제 설명이 굉장히 복잡하지만, 투포인터로 왼쪽 끝과, 오른쪽 끝부터 조건에 따라서 이동시키는것만 잘 구현하면 되는 문제이다.
턴을 서로 번갈아가면서 진행한다는 점만 주의해서 마지막에 출력만 잘 하면 된다.
아래는 제출코드이다.
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
int main(void) {
// For fast IO
cin.tie(NULL);
ios_base::sync_with_stdio(false);
int tc;
int n;
cin >> tc;
while(tc--) {
int candies[1000];
int s[1000] = {0};
cin >> n;
int a = 0, b = 0, cnt = 0; // alice, bob
int ap = 0, bp = n; // alice, bob
int prev = -1;
bool turn = true; // true면 엘리스차례, false면 밥차례
for(int i = 0; i < n; i++) {
cin >> candies[i];
if(i == 0) s[i] = candies[i];
else s[i] = candies[i] + s[i - 1];
}
a += candies[0];
prev = a;
cnt++;
turn = false;
if(n == 1) {
cout << cnt << " " << a << " " << 0 << "\n";
continue;
}
// ap : 앨리스가 이미 "먹은" 포인터
// bp : 밥이 이미 "먹은" 포인터
while(ap < bp) {
int curCandies = 0;
if(turn) {
// 앨리스차례
while(curCandies <= prev) {
ap++;
if(ap >= bp) break;
curCandies += candies[ap];
}
prev = curCandies;
a += prev;
cnt++;
turn = !turn;
} else {
// 밥차례
while(curCandies <= prev) {
bp--;
if(bp <= ap) break;
curCandies += candies[bp];
}
prev = curCandies;
b += prev;
cnt++;
turn = !turn;
}
}
cout << cnt << " " << a << " " << b << "\n";
}
return 0;
}E번 Special Elements - 대회 이후 성공
길이 n인 정수배열 a가 주어진다. 배열 a의 각각의 원소에 대해서, 해당 원소가 배열 a의 l번째 원소부터 r번째 원소까지의 합과 같다면, 해당 원소는 특별하다(Special)고 할 수 있다. 배열이 주어졌을 때, 특별한 원소의 개수를 출력하시오.
정수 배열의 크기가 8000까지이고, 각각의 원소의 크기도 8000 이하의 자연수이다.
즉, 모든 (l, r) 조합을 확인하면서 최악의 경우 시간복잡도를 생각해보면,

l == 1 일 때, l < r 이므로, 최대 (n - 1)번 돌 것이다.
l == 2 일 때, 마찬가지로, 최대 (n - 2)번 돌 것이다.
이 과정을 반복해서, l == (n - 1)일 때, 1번 돌 것이므로, 모든 (l, r)조합을 탐색해도 시간이 초과되지 않는다.
대신에 (l, r)이 주어졌을 때, 그 사이의 원소의 합을 빠르게 구해야 하므로, 구간합을 이용할 것이다.
코드에서 secsum[i]는 0번째부터 i번째 원소까지 모든 원소의 합을 더한 값으로,
l부터 r까지의 합은 secsum[r] - secsum[l - 1]로 나타날 수 있다.
이때 구하려는 것은, 원소가 Special한지를 확인하는 것이다. 즉, l부터 r까지 더한 값이 원소의 범위인 1부터 8000사이의 값이 아니라면, 저장할 필요가 없으므로 건너 뛰고, 만약 범위 내에 있다면, isSpecial이라는 배열에 true로 저장한다.
이후 1부터 8000까지 탐색하면서 isSpecial에서 true인 값을 카운트해주면 정답이 된다.
아래는 제출코드이다.
#include <bits/stdc++.h>
// 2의 제곱수 판정
#define POW2(X) (X) == ((X)&(-(X)))
// 기본설정
typedef long long ll;
using namespace std;
int dirx[4] = {1, 0, -1, 0};
int diry[4] = {0, 1, 0, -1};
int main(void) {
cin.tie(NULL);
ios_base::sync_with_stdio(false);
int tc;
cin >> tc;
while(tc--) {
int n, ans = 0; cin >> n;
int arr[n];
bool isSpecial[8000 + 1] = {false};
int secsum[n + 1] = {0};
for(int i = 0; i < n; i++) {
cin >> arr[i];
if(i == 0) secsum[i] = arr[i];
else secsum[i] = secsum[i - 1] + arr[i];
}
for(int l = 0; l < n; l++) {
for(int r = l + 1; r < n; r++) {
int stt, dst;
if(l == 0) stt = 0;
else stt = secsum[l - 1];
dst = secsum[r];
if(dst - stt <= 8000) isSpecial[dst - stt] = true;
}
}
for(int i = 0; i < n; i++) {
if(isSpecial[arr[i]]) ans++;
}
cout << ans << "\n";
}
return 0;
}
F번 Special Elements - 대회 이후 성공
0과 1로 구성된 문자열이 있다. 이 문자열에서 인접한 원소의 0의 개수에 따라 n0, n1, n2를 정할 수 있다. n0, n1, n2가 주어졌을 때, 반대로 문자열을 출력하시오.
조건에 맞게 구현을 잘 하면 되는 문제이다.
코드에서는, "11"을 가장 앞에, 그 다음에 "00"을, 마지막으로 "01" 또는 "10"을 배치하였다.
왜냐하면 "11"과 "00" 또는 "01" 사이에서 "10"이 반복되기 때문에 n1을 카운트하는데 어려움이 있어서, 최대한 겹치는 위치를 줄이기 위해, "11"을 앞에서 모두 사용한 후, "10"이 한번 겹치더라도 이후에 바로 "00"을 출력하였다. 그리고 나머지 n1만큼 "1"과 "0"이 반복되게 출력하면 된다.
이 경우, 만약 n2나 n0중에 하나라도 없는 경우, 즉 앞에서 "10"이 겹치는 경우가 없는 경우만 따로 예외처리로 처리해주었다.
n2와 n0의 경우, "1"과 "0"을 각각 (n2 + 1)번, (n0 + 1)번 출력하면 개수가 맞는다.
만약 n2 또는 n0이 0이라면, n1케이스가 앞에서 한번 겹치므로 n1을 1 빼주고 계산한다.
n1의 경우 "10" 또는 "01"을 (n1 / 2)번 출력하고, n1이 홀수라면 "0" 또는 "1"을 한번 더 출력한다.
"10"으로 시작하는 경우는, n0이 0이 아닌 경우이고, "01"으로 시작하는 경우는, n0이 0인 경우이다.
아래는 제출코드이다.
#include <bits/stdc++.h>
// 2의 제곱수 판정
#define POW2(X) (X) == ((X)&(-(X)))
// 기본설정
typedef long long ll;
using namespace std;
int dirx[4] = {1, 0, -1, 0};
int diry[4] = {0, 1, 0, -1};
int main(void) {
cin.tie(NULL);
ios_base::sync_with_stdio(false);
int tc;
cin >> tc;
while(tc--) {
int n0, n1, n2;
cin >> n0 >> n1 >> n2;
// 111100001010 모양으로 출력
// n2가 0일 경우, 앞에서 n1을 한번 처리하지 못함.
// 마찬가지로 n0이 0일경우 앞에서 n1을 한번 처리하지 못함.
if(n2 == 0) {
for(int i = 0; i < n0 + 1; i++) cout << "0";
for(int i = 0; i < n1 / 2; i++) cout << "10";
if(n1 % 2 == 1) cout << "1";
} else if(n0 == 0) {
for(int i = 0; i < n2 + 1; i++) cout << "1";
for(int i = 0; i < n1 / 2; i++) cout << "01";
if(n1 % 2 == 1) cout << "0";
} else {
// 나머지 경우 출력
for(int i = 0; i < n2 + 1; i++) cout << "1";
for(int i = 0; i < n0 + 1; i++) cout << "0";
// n2와 n0 사이에서 n1 경우가 한 개 발생함.
// n1을 처리하는 시작부분은 무조건 1
n1--;
for(int i = 0; i < n1 / 2; i++) cout << "10";
if(n1 % 2 == 1) cout << "1";
}
cout << "\n";
}
return 0;
}G번 Special Permutation - 대회 이후 성공
순열 P가 주어진다. 배열의 원소를 재배치하여, 인접한 두 배열의 차이가 2와 4 사이가 되도록 하려고 한다. 이때의 순열을 출력하거나, 만들 수 없는 경우 -1을 출력하시오.
Div4의 G번이라 그런지 어려운 문제는 아니였다.
문제에서 차이값의 최솟값이 2이므로, 홀수는 홀수끼리 1, 3, 5, ... 그리고 짝수는 짝수끼리 2, 4, 6, ... 배치하면 2씩 차이나게 할 수 있다. 가장 쉬운 아이디어는, 앞쪽에는 짝수를, 뒤쪽에서는 홀수를 배치하는 경우이다.
홀수의 경우 맨 앞의 숫자가 1이라고 가정하면, 1의 좌측에 4를 위치시킨다. (차이 : 3)
그리고, 4의 좌측에 짝수 중 가장 작은 수인 2를 배치시킨다. (차이 : 2)
이후 짝수 각각의 좌측에 6부터 n보다 작은 가장 큰 짝수까지 배치시킨다, (차이 4, 이후 2)
예를 들면, n == 6인 경우, 6 2 4 1 3 5 와 같이 나타낼 수 있다.
그러나 불가능한 경우가 있는데, 1과 짝수사이의 차이가 2 ~ 4가 나려면 짝수 4가 꼭 필요하다. 만약 n이 4보다 작다면, 홀수와 짝수를 연결할 수 없으므로, 불가능하다. 이 경우만 예외처리하고, 출력만 잘 하면 맞는 문제이다.
아래는 제출코드이다.
#include <bits/stdc++.h>
// 2의 제곱수 판정
#define POW2(X) (X) == ((X)&(-(X)))
// 기본설정
typedef long long ll;
using namespace std;
int dirx[4] = {1, 0, -1, 0};
int diry[4] = {0, 1, 0, -1};
int main(void) {
cin.tie(NULL);
ios_base::sync_with_stdio(false);
int tc;
cin >> tc;
while(tc--) {
int n;
cin >> n;
vector<int> ans;
if(n < 4) {
cout << -1 << "\n";
} else {
for(int i = n; 4 < i; i--) {
if(i % 2 == 0) {
cout << i << " ";
}
}
cout << "2 4 ";
for(int i = 1; i <= n; i++) {
if(i % 2 != 0) {
cout << i << " ";
}
}
cout << "\n";
}
}
return 0;
}